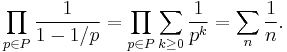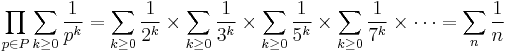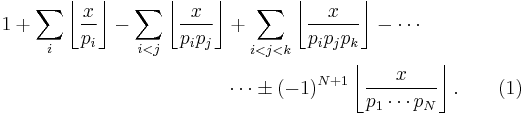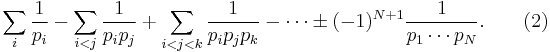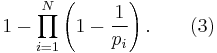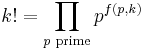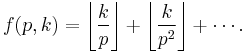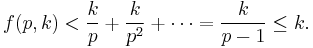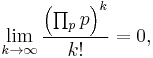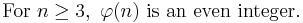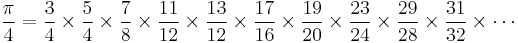Euclid's theorem

Euclid's theorem is a fundamental statement in number theory that asserts that there are infinitely many prime numbers. There are several well-known proofs of the theorem.

1 Euclid's proof
2 Euler's proof
3 FÃ¼rstenberg's proof
4 Some recent proofs
- 4.1 Pinasco
- 4.2 Whang
5 Proof using Euler's totient function
6 Proof using the irrationality of Ï
7 See also
8 Notes and references
9 External links

Euclid's proof

Euclid offered the following proof published in his work Elements (Book IX, Proposition 20)^[1] and paraphrased here.

Take any finite list of prime numbers p₁, p₂, ..., p_n. It will be shown that at least one additional prime number not in this list exists. Let P be the product of all the prime numbers in the list: P = p₁p₂...p_n. Let q = P + 1. Then, q is either prime or not:

If q is prime then there is at least one more prime than is listed.

If q is not prime then some prime factor p divides q. This factor p is not on our list: if it were, then it would divide P (since P is the product of every number on the list); but as we know, p divides P + 1 = q. Then p would have to divide the difference of the two numbers, which is (P + 1) â P or just 1. But no prime number divides 1 so there would be a contradiction, and therefore p cannot be on the list. This means at least one more prime number exists beyond those in the list.

This proves that for every finite list of prime numbers, there is a prime number not on the list. Therefore there must be infinitely many prime numbers.

It is often erroneously reported that Euclid proved this result by contradiction, beginning with the assumption that the set initially considered contains all prime numbers, or that it contains precisely the n smallest primes, rather than any arbitrary finite set of primes.^[2] Although the proof as a whole is not by contradiction, in that it does not begin by assuming that only finitely many primes exist, there is a proof by contradiction within it: that is the proof that none of the initially considered primes can divide the number called q above.

Euler's proof

Another proof, by the Swiss mathematician Leonhard Euler, relies on the fundamental theorem of arithmetic: that every integer has a unique prime factorization. If P is the set of all prime numbers, Euler wrote that:

$\prod_{p\in P} \frac{1}{1-1/p}=\prod_{p\in P} \sum_{k\geq 0} \frac{1}{p^k}=\sum_n\frac{1}{n}.$

The first equality is given by the formula for a geometric series in each term of the product. To show the second equality, distribute the product over the sum:

$\prod_{p\in P} \sum_{k\geq 0} \frac{1}{p^k}=\sum_{k\geq 0} \frac{1}{2^k}\times\sum_{k\geq 0} \frac{1}{3^k}\times\sum_{k\geq 0} \frac{1}{5^k}\times\sum_{k\geq 0} \frac{1}{7^k}\times\cdots=\sum_n\frac{1}{n}$

in the result, every product of primes appears exactly once, so by the fundamental theorem of arithmetic, the sum is equal to the sum over all integers.

The sum on the right is the harmonic series, which diverges. So the product on the left must diverge also. Since each term of the product is finite, the number of terms must be infinite, so there is an infinite number of primes.

FÃ¼rstenberg's proof

In the 1950s, Hillel FÃ¼rstenberg introduced a proof using point-set topology. See FÃ¼rstenberg's proof of the infinitude of primes.

Some recent proofs

Pinasco

Juan Pablo Pinasco has written the following proof.^[3]

Let p₁, ..., p_N be the smallest N primes. Then by the inclusionâexclusion principle, the number of positive integers less than or equal to x that are divisible by one of those primes is

$\begin{align} 1 %2B \sum_{i} \left\lfloor \frac{x}{p_i} \right\rfloor - \sum_{i < j} \left\lfloor \frac{x}{p_i p_j} \right\rfloor & %2B \sum_{i < j < k} \left\lfloor \frac{x}{p_i p_j p_k} \right\rfloor - \cdots \\ & \cdots \pm (-1)^{N%2B1} \left\lfloor \frac{x}{p_1 \cdots p_N} \right\rfloor. \qquad (1) \end{align}$

Dividing by x and letting x â â, we get

$\sum_{i} \frac{1}{p_i} - \sum_{i < j} \frac{1}{p_i p_j} %2B \sum_{i < j < k} \frac{1}{p_i p_j p_k} - \cdots \pm (-1)^{N%2B1} \frac{1}{p_1 \cdots p_N}. \qquad (2)$

This can be written as

$1 - \prod_{i=1}^N \left( 1 - \frac{1}{p_i} \right). \qquad (3)$

If no other primes than p₁, ..., p_N exist, then the expression in (1) is equal to 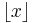$\lfloor x \rfloor$ and hence the expression in (2) is equal to 1. But clearly the expression in (3) is less than 1. Hence there must be more primes than p₁, ..., p_N.

Whang

Junho Peter Whang has recently published the following proof by contradiction.^[4] Let k be any positive integer. Then according to de Polignac's formula (actually due to Legendre)

$k! = \prod_{p\text{ prime}} p^{f(p,k)} \,$

where

$f(p,k) = \left\lfloor \frac{k}{p} \right\rfloor %2B \left\lfloor \frac{k}{p^2} \right\rfloor %2B \cdots.$

Note that

$f(p,k) < \frac{k}{p} %2B \frac{k}{p^2} %2B \cdots = \frac{k}{p-1} \le k.$

But if only finitely many primes exist, then

$\lim_{k\to\infty} \frac{\left(\prod_p p\right)^k}{k!} = 0,$

so that is impossible.

Proof using Euler's totient function

The theorem can be also proved by using Euler's totient function Ï.^[5] In this proof, the following property will be used:

$\text{For } n \ge 3,\ \varphi(n)\text{ is an even integer.}$

Assume that there is only a finite number of primes. Call them p₁, p₂, ..., p_r and consider the integer n = p₁p₂ ... p_r. Any natural number a â¤ n has a prime divisor q. Then, q must be one of p₁, p₂, ..., p_r, since that is the list of all prime numbers. Hence, for all a â¤ n, gcd(a, n) > 1 except if a = 1. This leads to Ï(n) = 1, which contradicts the property above.

Proof using the irrationality of Ï

The following formula was discovered by Euler.

$\frac{\pi}{4} = \frac{3}{4} \times \frac{5}{4} \times \frac{7}{8} \times \frac{11}{12} \times \frac{13}{12} \times \frac{17}{16} \times \frac{19}{20} \times \frac{23}{24} \times \frac{29}{28} \times \frac{31}{32} \times \cdots \;$

Each denominator is the multiple of four nearest to the numerator.

If there were finitely many primes, $Ï$ would be rational. This contradicts the fact that $Ï$ is irrational. However, to prove that $Ï$ is irrational is considerably more onerous than to prove that infinitely many primes exist.

Notes and references

^ James Williamson (translator and commentator), The Elements of Euclid, With Dissertations, Clarendon Press, Oxford, 1782, page 63.
^ Michael Hardy and Catherine Woodgold, "Prime Simplicity", Mathematical Intelligencer, volume 31, number 4, fall 2009, pages 44â52.
^ Juan Pablo Pinasco, "New Proofs of Euclid's and Euler's theorems", American Mathematical Monthly, volume 116, number 2, February, 2009, pages 172â173.
^ Junho Peter Whang, "Another Proof of the Infinitude of the Prime Numbers", American Mathematical Monthly, volume 117, number 2, February 2010, page 181.
^ David M. Burton, Elementary Number Theory, sixth edition, McGrawâHill, 2007, pages 134â135.

External links

Weisstein, Eric W., "Euclid's Theorem" from MathWorld.
Euclid's Elements, Book IX, Prop. 20 (Euclid's proof, on David Joyce's website at Clark University)